سری
در ریاضی سری عبارت است از مجموع جملات یک دنباله.به عبارت دیگر سری شماری از اعداد است که بین آنها عملگر جمع قرار گرفته است.
| ...+5+4+3+2+1 |
سریها بر دو نوعند:سریهای متناهی و نامتناهی؛که سریهای متناهی را می توان با اعمال ساده جبری محاسبه کرد،ولی برای محاسبه سریهای نامتناهی باید از آنالیز کمک گرفت.
به عنوان مثال سری زیر یک سری متناهی است.
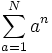
سری نامتناهی، سری میباشد که جملات آن محدود نیست.
به این سری توجه نمایید:

این سری یک سری عددی نامتناهی میباشد.که در حالت کلی به صورت زیر نشان داده میشود.که به آن سری هندسی میگویند.
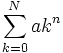
a را جمله اول و k را قدر نسبت سری می نامند.مجموع n جمله اول یک سری رابا
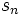 نشان میدهند
نشان میدهند
در صورتی که
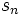 به سمت یک عدد متناهی سیر کند آن را همگرا مینامند. در غیر این صورت به آن یک سری واگرا گویند.
به سمت یک عدد متناهی سیر کند آن را همگرا مینامند. در غیر این صورت به آن یک سری واگرا گویند.
حال به معرفی نوع دیگری از سریها به نام سریهای توانی می پردازیم:سریهایی را که جملات آن توابعی از متغیر x باشند را سریهای توانی گویند.و مجموعه مقادیر از x که به ازای آنها توابع موجود در سری تعریف شده و سری همگرا باشد را میدان همگرایی سری گویند.
هر سری تابعی به شکل

را یک سری توانی بر حسب
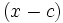 میگویند.واضح است که جملات آن به فرم زیردر میآید:
میگویند.واضح است که جملات آن به فرم زیردر میآید:
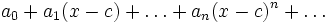 |
 را میتوان به صورت جمع توابعی بر حسب
را میتوان به صورت جمع توابعی بر حسب  نوشت.
نوشت.
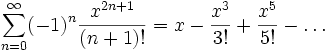
لازم به توضیح است که در سری فوق c=0 در نظر گرفته شده است.
تصاعد حسابی
تعریف:
اگر جمله عمومی یک سری بصورت باشد که در آن d , a عددهای ثابت و مستقل از n هستند، سری را تصاعد حسابی مینامیم. از تعریف
باشد که در آن d , a عددهای ثابت و مستقل از n هستند، سری را تصاعد حسابی مینامیم. از تعریف  بدست میآید:
بدست میآید: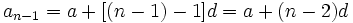
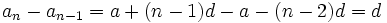
پس تفاضل هر دو جمله متوالی تصاعد حسابی مقدار ثابت d است. به همین سبب d را تفاضل مشترک تصاعد حسابی مینامند. همچنین به ازای n=1 ،
 . پس ، a جمله اول تصاعد حسابی است. بنابراین جملههای دیگر تصاعد حسابی با افزودن مقدار ثابت d به جمله پیش از آن بدست میآید.
. پس ، a جمله اول تصاعد حسابی است. بنابراین جملههای دیگر تصاعد حسابی با افزودن مقدار ثابت d به جمله پیش از آن بدست میآید. مجموع n جمله اول تصاعد حسابی
فرض میکنیم که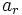 جمله rام تصاعد حسابی باشد، یعنی
جمله rام تصاعد حسابی باشد، یعنی 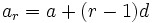 . می خواهیم
. می خواهیم 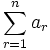 را که با
را که با  نشان داده میشود، حساب کنیم. اکنون ، سری دیگری میسازیم که در آن n جمله
اول تصاعد حسابی با ترتیب عکس قرار گرفته باشند سری جدید بصورت زیر است:
نشان داده میشود، حساب کنیم. اکنون ، سری دیگری میسازیم که در آن n جمله
اول تصاعد حسابی با ترتیب عکس قرار گرفته باشند سری جدید بصورت زیر است: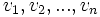
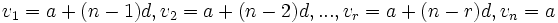
مجموع این سری همان مجموع n جمله اول تصاعد حسابی است. پس ،
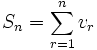
معمولا جمله nام ، یعنی
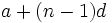 را با l نشان میدهیم. پس
را با l نشان میدهیم. پس 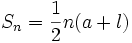
ویژگیها
- اگر عددی را به همه جملههای یک تصاعد حسابی اضافه کنیم یا از آنها کم کنیم یک تصاعد حسابی دیگر با همان تفاضل مشترک بدست میآید.
- اگر همه جملههای یک تصاعد حسابی در عددی ضرب یا بر عددی تقسیم شوند یک تصاعد حسابی دیگر با تفاضل مشترک متفاوت بدست میآیند.
تصاعد هندسی
به دنبالهای که رابطه بازگشتی آن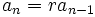 باشد یک دنباله هندسی یا تصاعد هندسی گفته میشود.
باشد یک دنباله هندسی یا تصاعد هندسی گفته میشود. 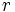 را قدرنسبت تصاعد هندسی مینامیم.
را قدرنسبت تصاعد هندسی مینامیم. اگر
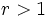 و
و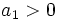 باشد، دنباله اکیداً صعودی خواهد بود و اگر
باشد، دنباله اکیداً صعودی خواهد بود و اگر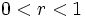 و
و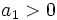 دنباله اکیداً نزولی خواهد بود.
دنباله اکیداً نزولی خواهد بود. رابطه صریح دنباله هم به صورت
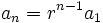 میباشد که واضح نیز به نظر میرسد.
میباشد که واضح نیز به نظر میرسد. مسألهای که در تصاعد هندسی قابل تأمل میباشد مجموع جملات آن است.
اگر
 را مجموع جملات
را مجموع جملات 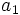 تا
تا  تعریف کنیم:
تعریف کنیم: 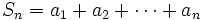
آنگاه
 دنبالهای با رابطه بازگشتی زیر خواهد بود:
دنبالهای با رابطه بازگشتی زیر خواهد بود: 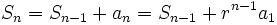
اما مقدار صریح
 نیز به سادگی قابل محاسبه میباشد که داریم:
نیز به سادگی قابل محاسبه میباشد که داریم: 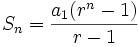
مثال:
اگر مجموع جملات دنباله هندسی با عنصر اول
مجموع جملات دنباله هندسی با عنصر اول 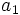 و قدرنسبت
و قدرنسبت 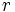 و
و 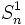 مجموع جملات دنباله هندسی دیگری با همان عنصر اول ولی قدرنسبت
مجموع جملات دنباله هندسی دیگری با همان عنصر اول ولی قدرنسبت 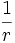 باشد. رابطه
باشد. رابطه  و
و 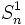 را بدست آورید؟
را بدست آورید؟ حل .
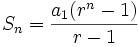
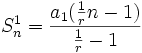
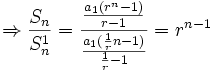
سری تیلور :
به وسیلهٔ بسط تیلور ( Taylor series)، میتوان توابع بینهایت بار مشتقپذیر را به صورت توابع توانی نوشت، و یا به عبارتی، بسط داد.
تعریف: اگر  در همسایگی
در همسایگی  و
و  بینهایت بار مشتقپذیر باشد، آنگاه
بینهایت بار مشتقپذیر باشد، آنگاه  را میتوان به صورت توانهایی از
را میتوان به صورت توانهایی از  نوشت.
نوشت.

که در اینجا،  مشتق n-اُم تابع
مشتق n-اُم تابع  است. این بسط به نام ریاضیدان انگلیسی بروک تیلور اسمگذاری شده است. این بسط برای همهٔ توابع حقیقی انجامپذیر نیست.
است. این بسط به نام ریاضیدان انگلیسی بروک تیلور اسمگذاری شده است. این بسط برای همهٔ توابع حقیقی انجامپذیر نیست.
مثال:

در همسایگی ۱- بینهایت بار مشتقپذیر است.
میتوان گفت:
همچنین، از بسط تیلور میتوان برای حل از روش سریهای توانی استفاده کرد .
حالت خاص سری تیلور که در پیرامون نقطه ۰ میباشد را سری مکلورن میگویند.
موارد پر کاربرد
لگاریتم:
دنباله هندسی نامتناهی:
متغیرهای دنباله هندسی نامتناهی:
ریشه مربع:
آزمون های همگرایی سریها را در ادامه مطلب ببینید.







 انسان هم می تواند دایره باشد هم خط راست.
انسان هم می تواند دایره باشد هم خط راست.